++ 50 ++ 等差数列の和 末項 333671-等差数列の和 末項

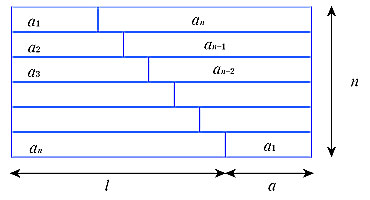
23/1/18 等差数列の和（具体例） 次のような等差数列を考えてみましょう。\ 1,4,7,10,13,16,19 \これは、初項が $1$ で、公差が $3$ 、項数が $7$ の等差数列です。この数列の和を考えてみましょう。 もちろん、前から順番に足していく、という方法もあります。13/1/21 等差数列の和の公式 (初項末項)×(項数/2) もう少し複雑になったものです。 同じようにして解くことができます。 赤い枠の中を見てください。それぞれの列(縦の2個)の数字の和は、どれも同じ数になっています。154です。等差数列の和S_nは S_n=(n/2){2a(n1)d} ※初項a,公差d 初項と公差がわかっていれば任意の項までの和は求まります。 ですから、末項つまり第n項は求める必要はありません。 ちなみに、 等差数列の一般項a_nは a_n=a(n1)d

2

等差数列の和 末項

等差数列の和 末項- このノートについて ちー 等差数列 等差数列の和 末項 初項 公差 数列 漸化式 数学的帰納法 帰納法 このノートが参考になったら、著者をフォローをしませんか？ 気軽に新しいノートをチェックすることができます！対象高校生 再生時間941 説明文・要約 ・等差数列の和は、(初項＋末項)×項数÷2 ・これを元に、等差数列の初項から第n項までの和を計算すると、{2a＋(n－1)d}n/2

Cms2 Chiba C Ed Jp Keiyo H Web E5 Ad A6 E6 A0 A1 Ef 81 81 81 Be 8c E5 8b E5 81 Ae E6 A3 Ae Ef 81 Ef Action Common Download Main Upload Id 4512

等差数列の和 等差数列の初項から第 n n 項までの n n 個の項の和を Sn S n とします。 Sn = a1 a2 a3 ・・・ an−1 an S n = a 1 a 2 a 3 ・ ・ ・ a n − 1 a n のことですね！ この和を簡単に求める公式があります。 等差数列の和 初項が a a で、末項が an等比数列の一般項は，植木算の関係で になりますが 等比数列の和()は ではありません．上記の中間項を消す解説図をよく見ると，末項（第 n 項） ar n−1 は消えて，代わりにそれに r を掛けた ar n が残ることが分かります． だから，正しいのは等差数列基本性质 （1）数列为等差数列的重要条件是：数列的前n项和S 可以写成S = 的形式 (其中a、b为常数)。 （2）在等差数列中，当项数为 时， ；当项数为 时， 。 （3）若数列为等差数列，则 仍然成等差数列，公差为 。 （4）若数列 均为等差数列

まとめ4 (等比数列の和) 初項 a, 公比 r，項数 n の等比数列の和 S n は ﾜﾝﾎﾟｲﾝﾄ 左の式で，r≠1のときの 末項と和の形に注意して 下さい。末項は r n1 ， 和は r n となっている ところに注意しましょう。 末項 ar n1 は第n項です。すなわち である。 初項a、公差d、項数nの等差数列の和をS n とすれば、 である。 ここでlは、この数列の最後の項（末項という）を表す。 とくに、奇数からなる数列1,3,5,のn項の和はn 2 である。 そして、一般項が項の番号nについての二次式であるような数列b 1 ,b 2 ,すなわちb n =An 2 BnCであるような数列については、その階差数列は等差数列であり、もし9/6/18 数列の和とΣ (シグマ)記号の意味と使い方 ＊この記事では、 等差数列の一般項 と 等比数列の一般項 は既知として、Σ公式やその証明などを解説していきます。 もし、分からなければ先に→ 等差数列と等比数列の一般項（漸化式の解き方） をぜひ読ん

1から100までを等差数列と考えると、初項が1、末項(一番最後の項)が100で、これを足すと101。 そしてこれが100項の半分50項あるので、101×50 つまり一般の等差数列n項の和は、(初項＋末項)×1/2n と一般に，初項 a，公差 d，項数 n の等差数列の末項を としますと，初項から第 n 項までの和 S n は， S n =a(ad)(a2d) ( d) (3) となります。等差数列の和の公式は２つありましたが、これら２つの公式の間には関係があります。 まず、末項 l は初項、交差、項数を用いて l = a (n − 1) d と表せます。 これを、公式： n 2 (a l) に代入すると、 n 2 { a a (n − 1) d } となり、公式２になります。

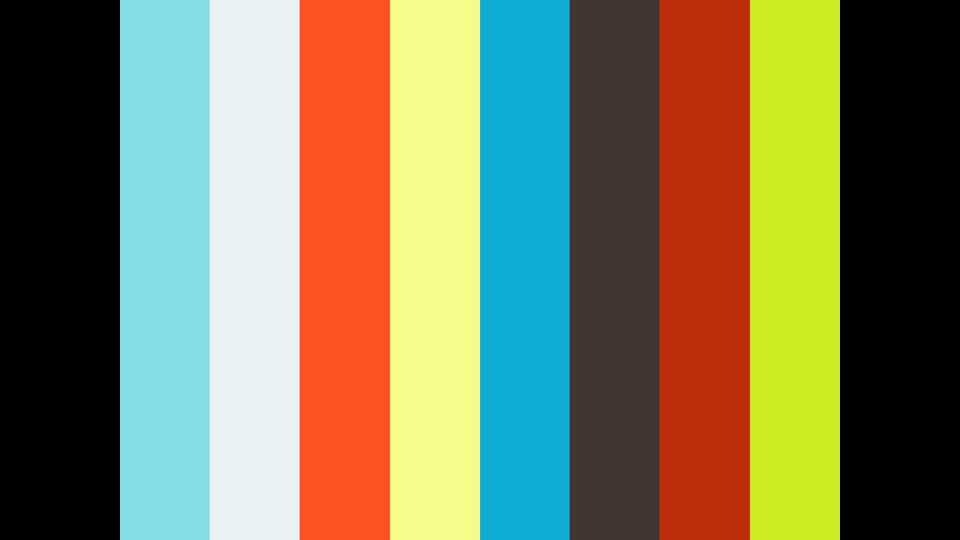
17 標準 途中からの倍数の和 中村 翔

1 3 37 9 2 7 42 1 Lihat Cara Penyelesaian Di Qanda

7/2/19 等差数列の和の公式 初項 \( a \)，公差 \( d \)，末項 \( l \)，項数 \( n \) の等差数列の和を \( S_n \) とすると \( \displaystyle \large{ \color{red}{ S_n = \frac{1}{2} n (a l) } } \) \( \displaystyle \large{ \color{red}{ S_n = \frac{1}{2} n \left\{ 2a (n1) d \right\} } } \)算数数学個別指導の中山先習塾の映像授業です。 高2「数列、等差数列、等差数列の和、初項末項を使う方法」 中山先習塾の公式サイト（ https 等差数列の和=ペアの和×ペアの数 「ペアの和」は、どのペアを選んでも同じなので、分かりやすいように「はじめの数と最後の数」で代表させましょう。 そして「ペアの個数」は10÷2 つまり「数字の個数÷2」でしたので、こういう公式ができます。 数列

高校数学b 等差数列を利用する倍数の和 受験の月

等差数列の和のイメージ Sicntech123 S Blog

26/5/18 こんにちは。 da Vinch (@mathsouko_vinch)です。 等差数列の和 等差数列は隣り合う項の差が等しい数列でした。では初項からある任意の項までの和を簡単に計算する術はあるのでしょうか。 まず、次の数列を考えるとこれは等差数列の公式は？3分でわかる公式、覚え方、等差数列の和の計算 等比数列の一般項は？1分でわかる求め方、和の計算、等差数列との違い 初項と第n項までの和の関係 下記に数列の和を求める公式を示します。いずれも初項aに関係する式ですね。 まとめ等差数列の和の公式 (A) 初項 a ，末項 l ，項数 n の等差数列の初項から末項までの和 S n は (B) 初項 a ，公差 d ，項数 n の等差数列の初項から第n項までの和 S n は ※どちらも アン（ a, n ）は必須 デル（ d, l ）は1つ選びます．

等差数列の公式まとめ 一般項 和の求め方をイチから学んでいこう 数スタ

等比数列の一般項と和 おいしい数学

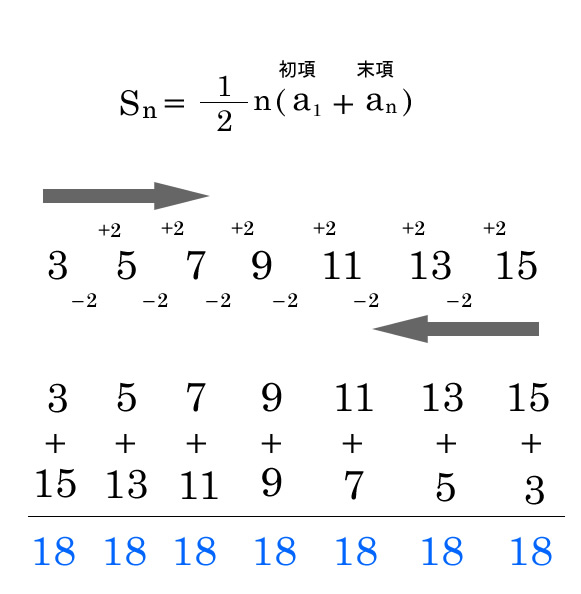
等差数列{3 , 5 , 7 , 9}の初項から第4項までの和は24となります。 3579=24 このように等差数列の和を求める問題はよく出題されます。6/3/21 等差数列 例： 2 4 6 ⋯ 100 = 2550 246\cdots 100=2550 2 4 6 ⋯ 100 = 2550 初項が a a a ，末項が l l l ，項数が n n n であるような等差数列の和は， 1 2 n (a l) \dfrac{1}{2}n(al) 2 1 n (a l) →等差数列の和の公式の例題と証明など 等比数列 例： 1 2 4 8 16 = 31 =31 1 2 4 8 16 = 3121/7/15 等差数列の和の公式は覚えずに、自分で15秒で作ろう♪ 4, 10 ,16, 22, 28, ・・・・・ のような等差数列があります。 78番目までの和 はいくつですか

等差数列の一般項と和 おいしい数学

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

23/6/21 等差数列の和は公式を言葉で覚えて「 初項 」「 末項 」「 項数 」から求めている意識が重要です。 ちなみに，教科書には $\displaystyle\frac{1}{2}n\left\{2a(n1)d\right\}$ という公式があるけど，使うことはないので覚えなくていいです。等差数列の和の公式は \(等差数列の和)=\frac{項数}{2}\times\left((初項)(末項)\right)\ と覚えておくとよい．つまり，等差数列の和は「項数」と「初項」と「末項」という3 つの要素がわかれば求めるこ等差数列 14, 21, 28, 35, 42, ⋅ ⋅ ⋅ の一般項 a n 、初項から第15項までの和 S 15 を求めよ。 答 S 15 = 945 方針 等差数列の一般項の公式より、 初項を a 1 、交差を d 、 一般項を a n とする。 a n = a 1 (n − 1) d を用いる． 次に初項から第15項までの和 S 15 は

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

Http Www Kodaira H Metro Tokyo Jp Site Zen Content Pdf

等差数列（とうさすうれつ）の一般項を求める公式は「an=a (n－1)d」です。 また、等差数列の和の公式はn (aan)/2で算定されます。21/4/12 １～１０までの和を求めます。 S= 1 2 3 4 5 6 7 8 910 これを① Sが等差数列の和 S=10 9 8 7 6 5 4 3 2 1 これを② ここで、上下を足すと、 2S= この11は、（初項＋末項） これが、項数（10）足されている。この等差数列の総和が 100 となるとき，𝑛 の値を求めよ。 初項 −5，末項 15，項数 𝑛 2 の等差数列の和が 100 であるから 1

数学切り抜き帳

等差数列 等比数列 優技録

等差数列の場合、第1項と第8項の和＝第2項と第7項の和＝3項と6項の和・・・になります。 この数列は、3,6,9,12,15,18,21,24なので、 （324）＝（621）＝（918）＝（1215） という関係になります。 従って、和は、になります。 これを一般化すると 初項をa、末項等差数列の和 初項 a ，末項 l ，項数 n である等差数列の和 S n は， この公式は，「台形の面積の公式と同じ」と覚えるとよい．等差数列の和 初項から n 番目の数までの和を表す Sn は、次の一般式(公式化した式)に当てはめれば求められる。 初項と末項をたして、それに項数を掛け、さらにその全体を2で割ればよい。例えば、5から21まで(5と21を含む)の奇数の和は、この間に奇数は5, 7, 11, 13, 15, 17, 19, 21の8つの項があるから、

項数を求めるときは 末項ー初項 1ですよね 赤線部は 初 Yahoo 知恵袋

研修室ブログ トーテックアメニティ株式会社

2．等差数列1;5;9;¢¢¢¢¢¢ において, 第6 項から第 項までの和を求めよ。 3．第9 項が14 , 第 項が47 となる等差数列の第9 項から第 項までの和を求 めよ。 4 初項が48 , 公差が¡3 である等差数列について第何項までの和が最大になるか。等差数列の和 1からウン千までのランダムな整数を並べたデータに、被りや欠落が無いかを確認するために利用させていただきました。 お年玉 (年齢×1000)の総額計算に！ 1から397までの和を求めるため、等差数列計算を利用。 等差数列をなす3つの数を等差数列の応用 問題 1260 以下の整数のうち， 7 で割り切れる数の和を求めよ． 答 S = 方針 等差数列の一般項の公式より， 初項を a 1 ，交差を d 、 一般項を a n とする． a n = a 1 (n − 1) d を用いる． 次に初項から末項までの和 S l は，等差数列の和

Cms2 Chiba C Ed Jp Keiyo H Web E5 Ad A6 E6 A0 A1 Ef 81 81 81 Be 8c E5 8b E5 81 Ae E6 A3 Ae Ef 81 Ef Action Common Download Main Upload Id 4512

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

等差数列の和の公式は \(等差数列の和)=\frac{項数}{2}\times\left((初項)(末項)\right)\ と覚えておくとよい．つまり，等差数列の和は「項数」と「初項」と「末項」という3 つの要素がわかれば求めるこ15/3/21 初項a、末項l、項数nの等差数列の和S n を求める公式は以下。 この公式についても具体的な数列を使いながら証明していきたい。 ＜公式の証明＞ 数列の代表例その2 ～等比数列と公式について～ 等差数列と同じく、数列の代表例である「等比数列」。

高校数学 B 数列 7歳の子が考えた等差数列の和を求める方法 やはり俺の考察ブログはまちがっている アニメ 数学

等比数列の和 初項 公比 末項

数学の天才 ガウス少年 等差数列の和の公式の考え方 スモビュ

等差数列 等比数列 優技録

2

数列５ 等差数列の和の公式は不要 ３ 怜悧玲瓏 高校数学を天空から俯瞰する

数列の基本２ 等差数列の和の公式 と 等比数列の和の公式

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

左のの公式は 末項がわかる場合のみに使える公式ということで右 Yahoo 知恵袋

A 1 N Lihat Cara Penyelesaian Di Qanda

2

等差数列の和 久保塾 今治市の学習塾

等差数列の和の公式の例題と証明など 高校数学の美しい物語

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 5 8

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

等差数列の和の公式の証明を超分かりやすく解説するよ

2

D 12 2 3 4 N 1 N N 123nd Descubre Como Resolverlo En Qanda

この S とsn ってなんの違いがあるんですか 末項なのか公差の違いですか Clear

Unilab Gbb Jp Math Ia Pdf Na010 Pdf

等差数列の一般項と和 おいしい数学

Www Pen Kanagawa Ed Jp Isehara H Zennichi Zaikouseihogosha Em Task Documents Suub Kaitou7 Hattenn Pdf

高校数学b 等差数列 A N の和 １ 映像授業のtry It トライイット

等差数列の和の公式

等差数列 数学の偏差値を上げて合格を目指す

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 5 8

倍数の和 等差数列の利用 大学受験の王道

高校数学b 等比数列の和の公式の証明 受験の月

第10講 For文以外の繰り返し ループ 処理 第６話 Do While文による末項が指定された値以下である等差数列の和

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 5 8

1

高校数学 B 数列 7歳の子が考えた等差数列の和を求める方法 やはり俺の考察ブログはまちがっている アニメ 数学

1

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

この数列の問題なんですが末項が4 2n 1になる理由と項数がnになる理由 大学受験 教えて Goo

等差数列 下 Sonicacts Com

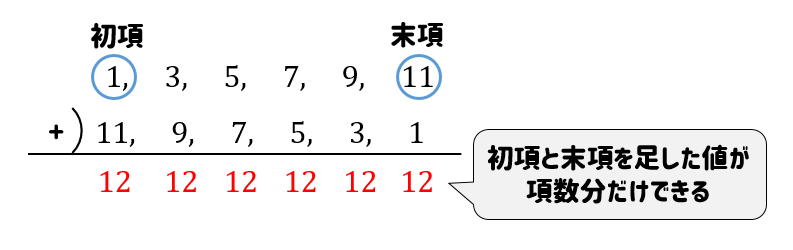
なぜ初項と末項が丸で囲ったようになるのですか Clear

第４講 同じことの繰り返し For文の学習 第４話 等差数列の和

48s96ub7b0z5f Net Tousa Suuretsu

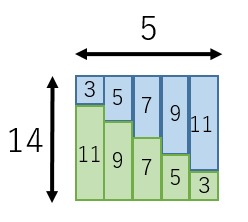
等差数列の和を計算する2つの公式 具体例で学ぶ数学

等差数列を徹底解説 一般項の求め方や和の公式をマスターしよう Studyplus スタディプラス

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

初項の求め方は 1分でわかる意味 等比数列と等差数列での求め方 一般項 末項との違い

等差数列 演習1 例題1 和の条件から初項と公差を求める 例題2 和の最大値を求める Youtube

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

1

等差数列の公式まとめ 一般項と和の公式を分かりやすく解説

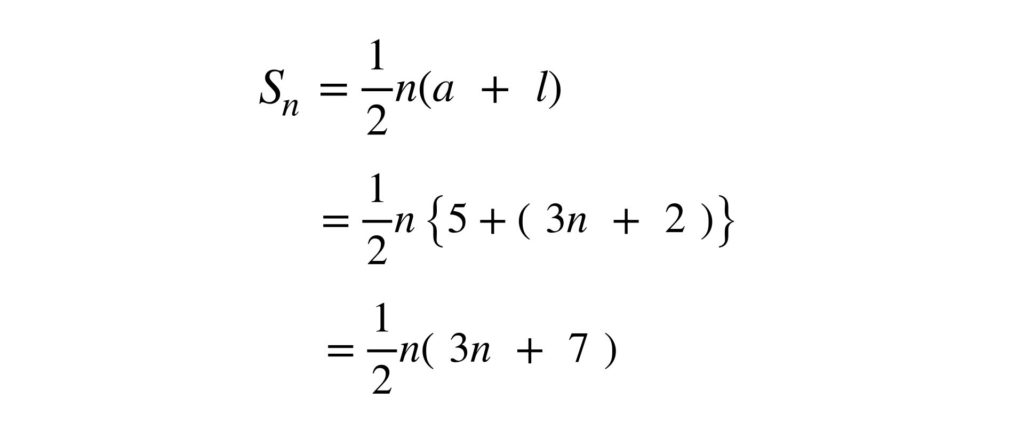
シグマの計算 苦手になるポイントを徹底解説 家庭教師の想い

等差数列の一般項や和の公式をマスターしよう ますますmathが好きになる 魔法の数学ノート

高校数学b 等差数列の和の公式 S N 1 2n A L 受験の月

Http Msnaka Sakura Ne Jp Mathb Point E6 95 B0 E5 97 81 Af E5 95 8f E9 A1 8c1 E8 A3 E7 Ad 94 Pdf

等差数列の性質と一般項と和の公式 等差数列の和は台形の面積 Irohabook

高校生 数学b 東京書籍 01 1章1節数列 等差数列の和 教科書解答解説 赤城 ᐡᐤᐡ

等比数列の和を求めよ 初項１ 公比２ 末項１２８お願いします Yahoo 知恵袋

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

第３講 繰り返し処理for文 第５話 Scanf によって 初項 交差 末項の値を取得して 等差数列の和を求めるアプリ

数列 等差数列の和 知能問題 数的処理 判断推理 数的推理 数学パズル ｓｐｉ 空間把握 解いてみてください

等比数列の和 初項 公比 末項

2 Diva Lihat Cara Penyelesaian Di Qanda

等差数列の公式は覚えずに 自分で15秒で作ろう

高校数学の等差数列の和の問題を学び直し 大学受験対策にも タロウ岩井の数学と英語 Note

シグマの計算 苦手になるポイントを徹底解説 家庭教師の想い

このように初項と公差と末項が分かっている時にはどうやって解いたらいいのですか Clear

数学用語解説 数b 数列

等差数列の和の問題について

私は2分の1 項数 初項 Clear

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

数学2b 等差数列の和の基本 レベル 4step 青チャ 無料プリント有 Youtube

等差数列の性質と一般項と和の公式 等差数列の和は台形の面積 Irohabook

2

3

高校数学b 等差数列 A N の和 １ 映像授業のtry It トライイット

数学b 数列の和 完全攻略チャート 実践例題集 自宅でできる受験対策ショップ ワカルー Wakaru

等差数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

等差数列 等比数列 優技録

数学b 数列 等差数列 和 オンライン無料塾 ターンナップ

等差数列の和 怜悧玲瓏 高校数学を天空から俯瞰する

等差数列 写真の問題を詳しく解説お願いします 私が習った等差数列の和 Yahoo 知恵袋

等差数列の和の公式の証明を超分かりやすく解説するよ

等差数列の公式まとめ 一般項 和の求め方をイチから学んでいこう 数スタ

1 N 3 N 13 N Lihat Cara Penyelesaian Di Qanda

等差数列の公式まとめ 一般項と和の公式を分かりやすく解説

等差数列の和

このように初項と公差と末項が分かっている時にはどうやって解いたらいいのですか Clear

一般項とは 1分でわかる意味 求め方 末項との違い 一般項の和との関係

等差数列の和の公式の証明を超分かりやすく解説するよ

Incoming Term: 等差数列の和 末項,